| An Induced Mental Block
A New Curriculum
|
|
We have all heard the frequent laments among our co-thinkers and professional colleagues at the sadly reduced state of science and mathematics education in our nation. As in all such matters, after the righteous indignation and hand-wringing, is over, one must ask oneself the realistic question: Are you part of the problem, or part of the solution?
If you are not sure, we have a proposal for you. To introduce it, I ask you to perform the following experiment.
STEP 1: As a suitable subject, locate any person who has attended high school within the last 50 or so years. You may include yourself. Now, politely ask that person, if he or she would please construct for you a square root.
“What do you mean construct a square root? I know what a square root is, but what do you mean ‘construct’ it?” is a typical answer from one sort of person.
“I was never good at math. I’m not a math person,” is the usual form of the other type response. Curiously, I have found that it is from this category of respondents that the correct solution is more likely to appear rapidly. In either case, some degree of resistance, tempered by a natural curiosity, is most often encountered at this point.
STEP 2: Remain calm, but resolute. Draw a square on a piece of paper, and ask the question again. “Here is a square, please show me the square root.”
Among the technically educated, it is very common, next, to see the diagonal of the square appear, often with the label 2 attached. As this has nothing whatsoever to do with the solution, I have found it most effective to point out in such cases, that the problem is really much simpler than that. No knowledge of the Pythagorean Theorem, nor any higher mathematics, is required.
A discussion of what is meant by a square root may now prove useful. I mean a very simple discussion. At this point, from among that second category of subjects, I have seen the light bulb go on rather quickly in a few cases. From the technically educated category, I have most often encountered a furious spurt of calculating and sketching, to no good end, sometimes followed by resignation. But, with persistence, these too will solve it. The exercise of constructing the square and rectangular numbers, as Theaetetus describes it in Plato’s dialogue of that name, can serve as a useful flank on the mental block encountered.
An Induced Mental Block
What is the problem? No student of the classical method of education, which has been around for at least the past 2,500 years, could ever have any problem with this simple exercise. The mental block which arises here is the perfectly lawful result of the absurd and prevalent modern-day teaching that number can exist independent of any physically determining principle. This is the ivory-tower view of mathematics, which holds sway from grade school to university, and reaches up like a hand from the grave, even into the peer review process governing what can be reported as the results of experimental physics.
This was the view that the young Carl Friedrich Gauss so devastatingly attacked in his 1799 “Proof of the Fundamental Theorem of Algebra,”1 submitted as his doctoral thesis to the University of Helmstedt. That every algebraic equation of degree m, where m is a positive integer, will have m roots, was a matter usually learned as a truism in any high school-level advanced algebra course, at least until the recent bad times. The proof of the assertion was not a matter one usually addressed. However, one has to take the student no further than the simple illustrative case x2+1=0 to cause a recognition of the essential paradox involved.
In the usual training, one is taught to write 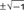 as the two solutions. as the two solutions.
“What is the square root of minus 1?”
“Ahem, that’s complicated; we may address that later.”
Mathematicians have known of this problem since at least 1545. In that year, Girolamo Cardano published a delightful account in Chapter XI of his Ars Magna. Here Cardan solves the problem “find two numbers whose sum is 10 and whose product is 40.” After showing us that the solutions must make use of the square roots of –15, Cardan examines what such a thing might be. Ask yourself: If a square root is the length of a side of a certain square number, what is the area of the square, the length of whose sides are negative? Finally, the Bolognese mathematician concludes his discussion of the paradoxical solution he has found (not without a bit of tongue in cheek, we presume): “This subtilty results from arithmetic of which this final point is, as I have said, as subtile as it is useless.”2
So the matter remained for two-and-a-half centuries. Despite the technically elegant proofs of the Fundamental Theorem of Algebra, provided successively by d’Alembert, Euler, and Lagrange, no resolution of the fundamental paradox of the existence of the ‘imaginary’ number had been made. As Bruce Director explains in the Pedagogy section of this issue (p. 66), Gauss’s new proof of the fundamental theorem, written at the age of 21, was an explicit and polemical attack on the shallow misconceptions of his celebrated predecessors. Gauss’s solution, which subsumes his creation of the complex domain, establishes the so-called imaginary numbers as perfectly lawful entities, with no handwaving required.
From that point onward, the sorts of sophistry, which still persist in the teaching and practice of this subject matter, were no longer necessary. The ivory tower practice of mathematics was no longer necessary, nor desirable. In its place must be the insistence which had always governed mathematics from the time of the Greeks, that nothing be accepted as true for which we could not provide a constructible representation.
This does not mean a crass empiricism. As Gauss showed for the case of the solution of algebraic functions, and as was already recognized in the writings of Plato, a higher concept of magnitude requires an act of the mind. That granted, nothing is to be accepted as true in mathematics, which does not correspond to a principle of physical action. “It works,” or “it is consistent with our defined set of allowable operations and procedures,” is, therefore, not acceptable. By accepting such shortcuts, first truth is destroyed, then science, then economies and whole nations.
A New Curriculum
Our proposal, suggested by Scientific Advisory Board member Lyndon H. LaRouche, Jr., is this. Let the mastery of Gauss’s fundamental theorem as developed in his revolutionary 1799 proof, serve as a cornerstone of a new curriculum for secondary and university undergraduate students. As LaRouche argued in motivating this proposal:
“Gauss’s devastating refutation of Euler’s and Lagrange’s misconception of ‘imaginary numbers,’ and the introduction of the notion of the physical efficiency of the geometry of the complex domain, is the foundation of all defensible conceptions in modern mathematical physics.… It also provides a standard of reference for the use of the term “truth,” as distinct from mere opinion, within mathematics and physical science, and also within the domain of social relations. Those goals are achieved only on the condition that the student works through Gauss’s own cognitive experience, both in making the discovery and in refuting reductionism generically. It is the inner, cognitive sense of ‘I know,’ rather than ‘I have been taught to believe,’ which must become the clearly understood principle of a revived policy of a universalized Classical humanist education.
“Once a dedicated student achieves the inner cognitive sense of ‘I know this,’ he, or she has gained a benchmark against which to measure many other things.”
We heartily concur, and urge our readers to join us in taking up the pedagogical challenge implied. Let the inspired item in our Pedagogy section serve as introduction. —Laurence Hecht
Notes
1. Carl Friedrich Gauss, “New Proof of the Theorem That Every Algebraic Rational Integral Function in One Variable Can be Resolved into Real Factors of the First or the Second Degree” (Helmstedt: Fleckeisen’s, 1799). English translation by Ernest Fandreyer, Prof. of Mathematics, Fitchburg State College available at: http://libraserv1.fsc.edu/proof/gauss.htm
2. Hieronimus Cardanus, Ars Magna (1545) ff. 65v. and 66r. transl. by Prof. Vera Sanford in D.E. Smith, A Source Book in Mathematics, (New York: Dover, 1959) pp. 201-202.
|